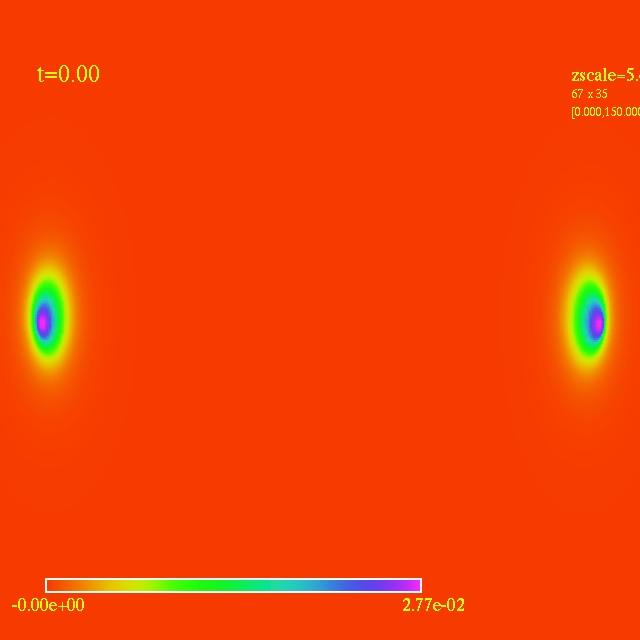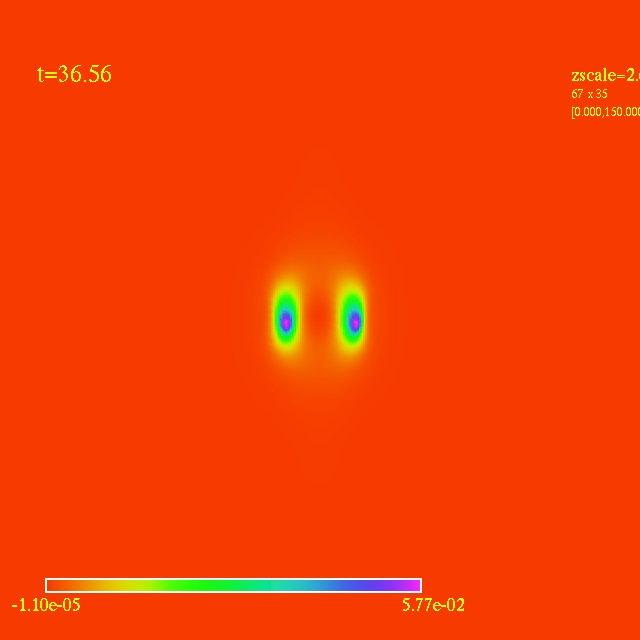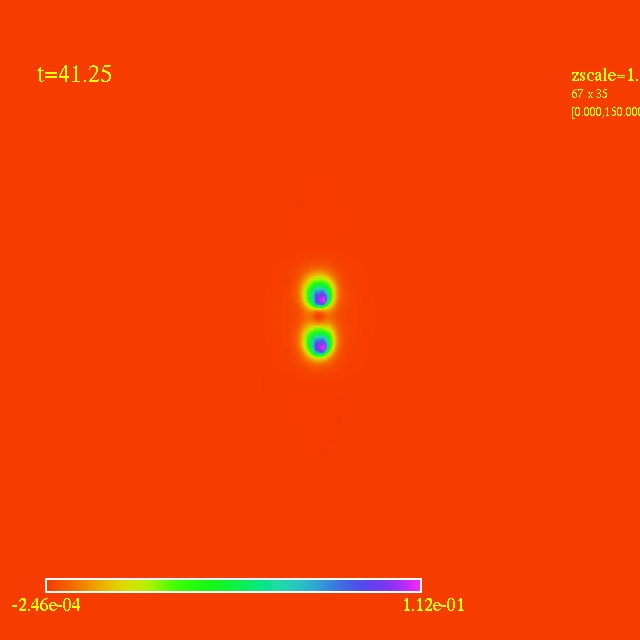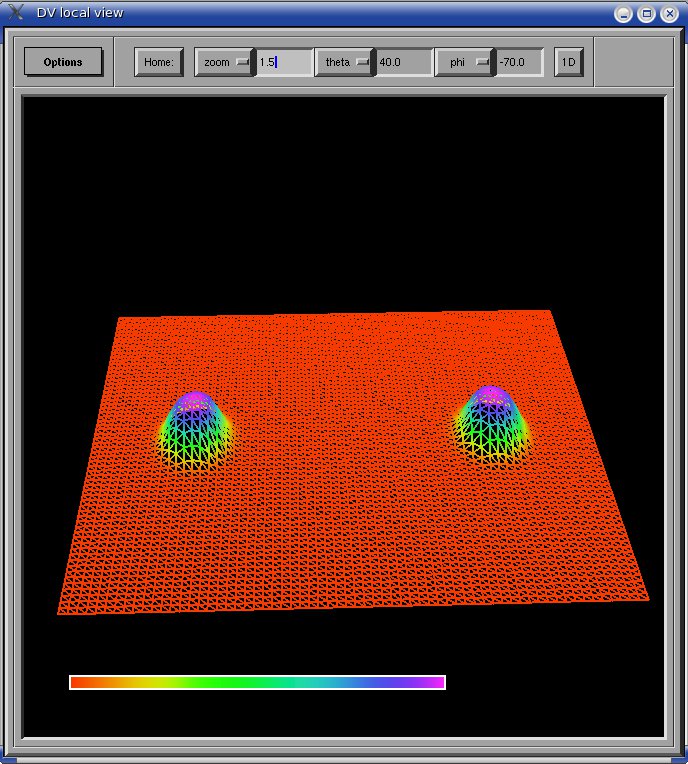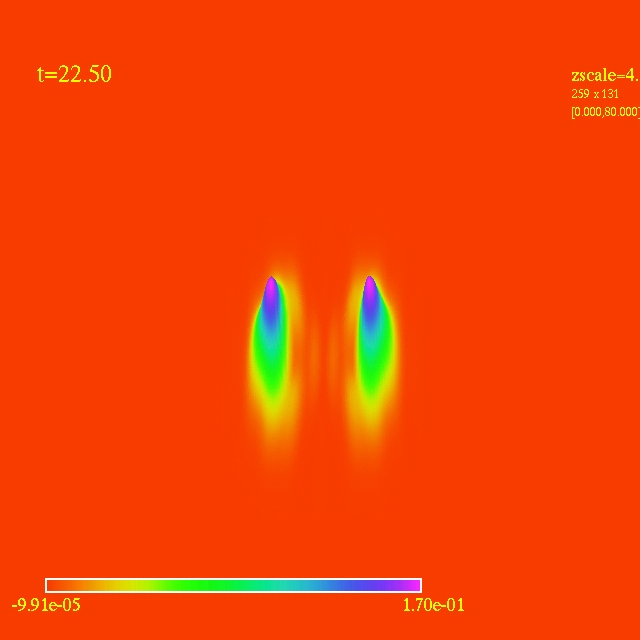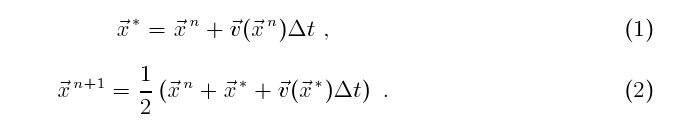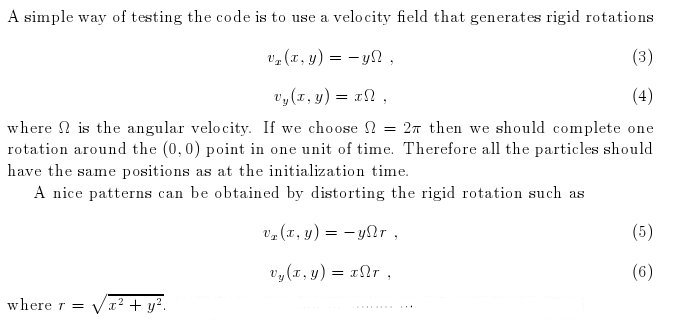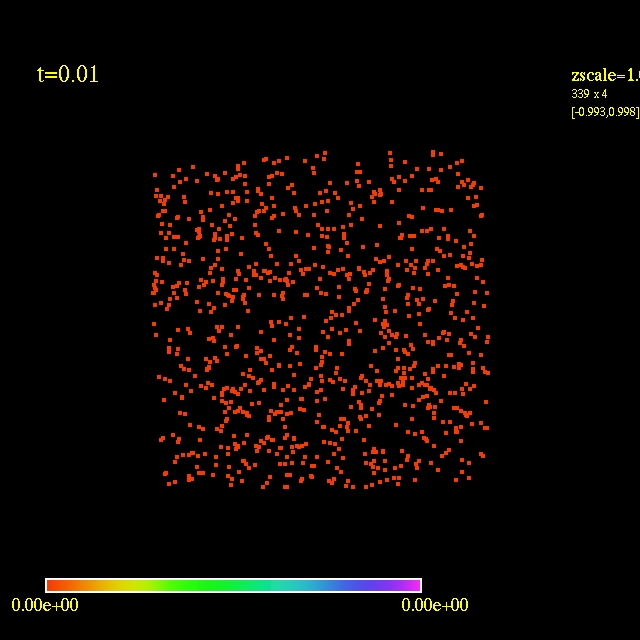 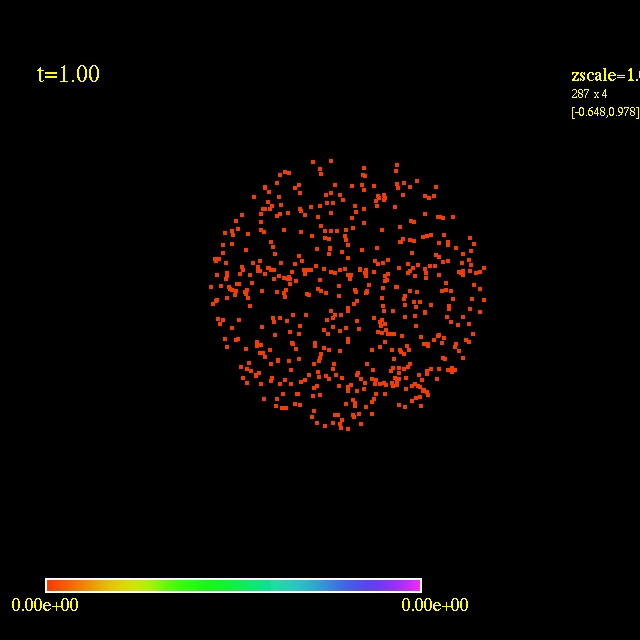
Left: initial configuration;
Right: end configuration with the analytic velocity field
independent of the radius.
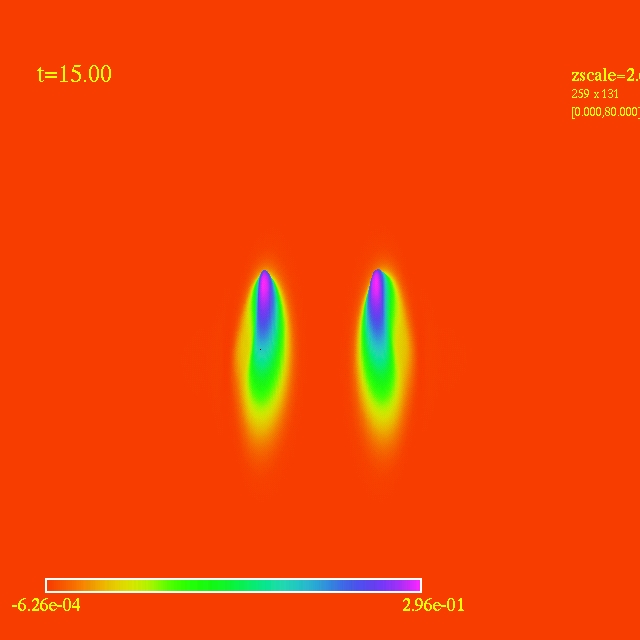
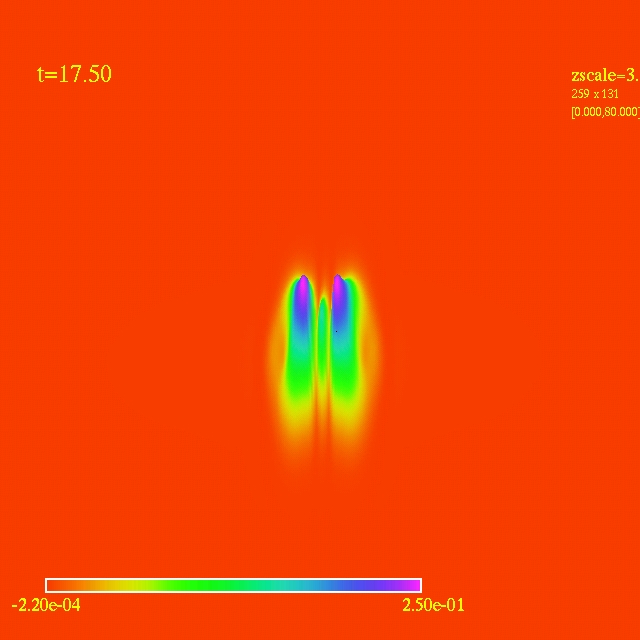
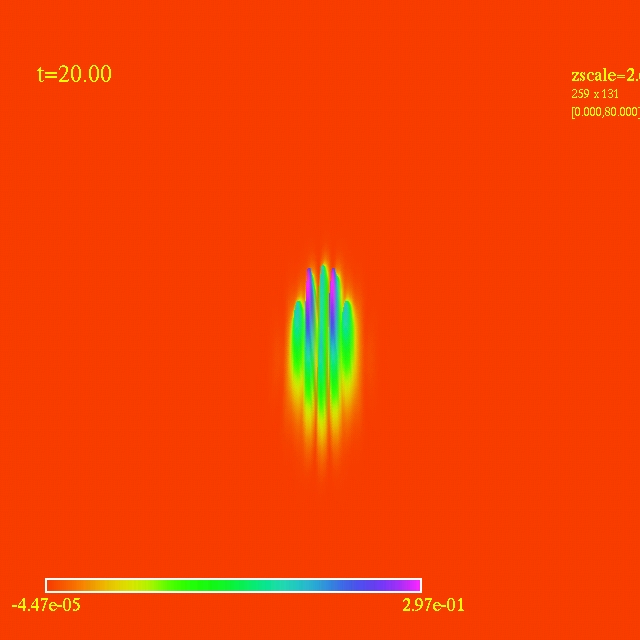
- Here I have some movies of the evolutions: (120 steps each)
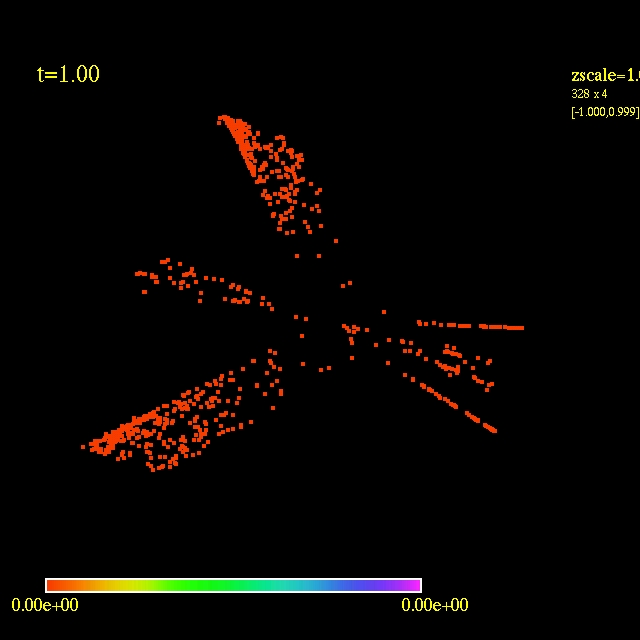
In this video the velocity
components of each of the 3000 particles in the configuration depends
as vx=sin(py/px) and vy=cos(py/px), where px and py are the x and y
positions of each particle respectively. They exit the domain in
Jet-like patterns.
This is a parallel
application to simulate the motion of test particles in a given
velocity field, for instance, the motion of smoke particles in the
wind.
Consider a 2D domain. The parallelization and domain
decomposition are
done by PAMR,
each
processor evolves the particles that currently
belong to its subdomain. Particles migrate from subdomain to subdomain
and also leave the domain completely. This approach is efficient as
long as the particles are approximately uniformly distributed over the
domain.
The domain is a square with the
left lower corner at (-1, -1) with its
center at (0, 0). We can evaluate the velocity field at each point of
the domain analitically , i.e., we know the functions vx (x, y) and vy
(x, y). I use a second order Runge-Kutta scheme to advance
each particle position from time level n to time level n + 1 by Δt,
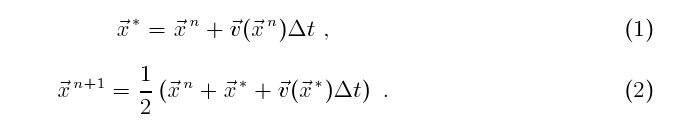
The next step is to migrate
particles that leave a
processor's subdomain into the corresponding new one. The
way implemented here is that each processor broadcasts the
positions of particles that left its
subdomain. Each processor then selects the particles belonging to its
subdomain. Note that in general the
domain is
not filled with particles uniformly, so that processors must handle
different number of them at a given time.
The bbhutils
offer an easy way for reading parameters from files,
Especially useful is the ivec type. The ivec type allows for easy and
compact notation of specifying an index vector. This is useful for
output control. The next snippet of code shows how to use the variable
out ivec to control the output frequency. The parameter file is passed
as the first command line argument.
The data can be viewed by DV
by selecting the item Particles from the options menu of the DV local
view window. The following is an example of a C routine that saves a 2D
particle data:
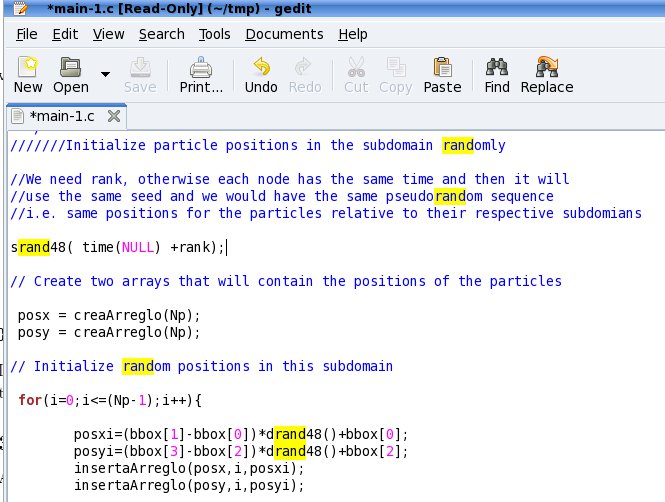
The particle positions are initialized randomly generating particles
within a desired domain.
 Source Code
Source Code
- The code consists in a main.c
program written in C, that uses PAMR calls and standard MPI calls. The
file fortran.f
contains the subroutines initialize, save_particles and make_step.
As
a
template
i
used
on of Martins examples of the course, one of the
unigrid codes.
- The number of particles in each subdomain is the same, Np;
PAMR
performs the subdivision. The particles are initialized randomly. I
need the rank, otherwise each node has the same time and then it will
use the same seed and we would have the same pseudorandom sequence i.e.
same positions for the particles relative to their respective
subdomains srand48( time(NULL) +rank);
- The make_step subroutine is written in fortran,
along
with a bunch of other subroutines found in the same file fortran.f
- the parameter file id
provides the type of velocity field to be used, the number of particles
and the number of time steps to be performed. The actual time step
length is defined inside the program.
- I checked the subdivision looking at the bbox vertices when
I
started to write the program.
- As requested, the vtype variable indicates which
type
of velocity is used: 1)
analytic field independent of r, 2) analytic field dependent of r, 3)
grid velocity field; where r is the radius of the particle with respect
to the center.
Grid
Velocity
Field
- Instead of a known analytic velocity field, the
velocity can be defined only on a grid. The simplest model is a time
independent the velocity field. The velocity at any given point
use linear interpolation using
the four vertices that surround a given point, first interpolating in
the x-direction and then in the y-direction. Two ghost zones are
employed for buffering. Note that the time step should be
sufficiently small so that a particle from inside the domain does not
migrate beyond the buffer zone in the first Euler substep (1) (so we
can complete the Runge-Kutta step). This model can be used to visualize
fluid flows that are
calculated on a computational grid (of course in that case the velocity
field would be also time dependent). The higher the resolution of
the the grid the closer the results should be to the analytic
profile.
- The grid velocity field is implemented: I made sure
particles dont make a large first RK step so they go out of the ghost
cells (I use two), so the program can calculate the velocity for the
second RK step; in main.c I set up a grid velocity field using two
arrays. I populate vx and vy on the grid using the analytical field
independent of r (of course the grid can store arbitrary values of vx
and vy). I was not able to use PAMR completely for this matter. So I
created the grid manually using arrays and then I pass it to the
make_step fortran subrotuine; then the velocity is interpolated from
the grid values and calculated at any arbitrary point of the subdomain.
This still needs work to do.
Architecture of the
code
- The total number of particles NT is divided by the
number of
processors p; PAMR subdivides the domain in p subdomains each with Np
particles and the positions are initialized randomly.
- A set of array-like data structures are defined
to
deal with dynamic arrays in an easy way (for me). I
began using these data structures but they turned out not to be very
flexible in some situations so they appear mixed with ordinary
dynamical arrays.
- We start the evolution: we create arrays posx and posy
to store the positions of the particles of each subdomain; we save the
particle positions here to sdf files.
- The
particle positions are evolved using a Runge-Kutta second order scheme
as requested; if the particle does not belong to the domain any more it
is placed in two migration arrays mx,my; posx and posy are
shrinked to a new size (creating and destroying arrays dynamically).
- Given the fact that the sizes of mx,my are different for
each
processor, I designate a master processor (the rank=0 cpu) so it uses a
MPI_Gather call to gather all the sizes of the
migration
arrays
from each processor; the sum of all sizes is totalN, so the master
processor creates recvArrayx and recvArrayy to allocate the migrants
positions.
- The master processor uses two MPI_Gatherv calls
to
gather the x and y positions of all migrants from all processors and
populate recvArrayx and recvArrayy.
- The
migrants arrays are broadcasted to all processors; in order for them to
allocate the migrants positions, totalN is broadcasted to all
processors so each creates two arrays for the "newcomers".
- We advance t=t+dt;
- Each processor takes those
migrants which belong to its subdomain; then each node merges the
newcomers with those particles already in the domain and we obtain the
new posx and posy arrays; we save them to sdf and we make the next
runge-kutta step
- The process is repeated N time steps. All this involves
the
creation, resizing and destruction of lots of arrays.
Compiling and Running
the program
- My Makefile
- The process is the usual:
1 cd 2d
2 make clean
3 source /home3/vnfe4/home/benjamin/2d/soPGI-mpich
4 make
- id
is the parameter file:
- mpirun -np 3 -machinefile machfile
par2d.exe id
Scaling
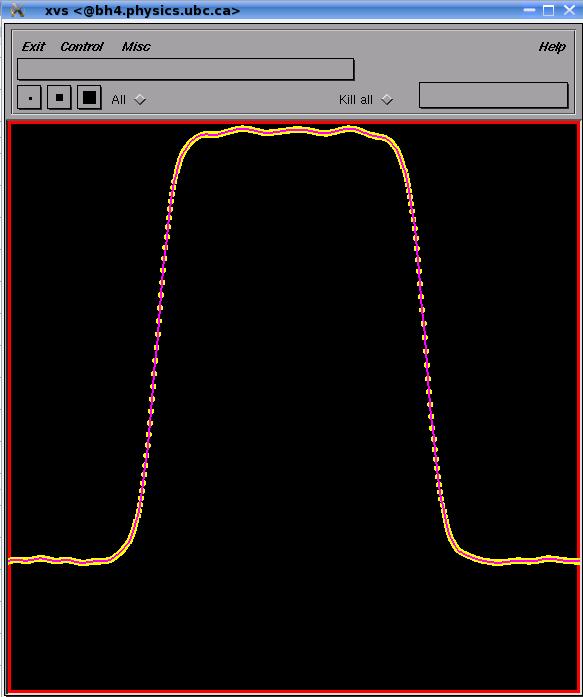
I
set the analytic velocity field so the particles go in circles; 1=N*dt
where N is the number of time steps and dt is the time-length of the
time step; the local error or a Runge-Kutta scheme of second order is
supossed to be proportional to dt^3, and the global error proportional
to dt^2; I was not sure about this and I decided to write a program
that would evolve a complete orbit of a single particle located at
radius=1 using this scheme; then i calculated the error of the radius
after the orbit and the relative error dr/r for different values of dt
and N time steps such that N*dt=1; the results are shown in this
file and the following graph. Starting from N=27 and dt=0.037, the
relative error is ~1%, so if we use a dt=0.01 and 100 or so
time steps, we are safely well below 1 percent of relative error in the
radius after one orbit.
So for the Scaling of the code I constructed the
following table (the times are measured in seconds using MPI_Wtime):
| Total Number Particles |
2 processors |
4 |
6 |
8 |
16 |
| 100 |
0.027017 |
0.461920 |
0.494730 |
0.67247 |
1.202543 |
| 1000 |
1.820399 |
1.888175 |
1.773452 |
1.981796 |
2.006310 |
| 10000 |
14.319587 |
8.407474 |
6.911991 |
7.149420 |
13.688003 |
| 100000 |
340.282804 |
286.478503 |
289.795620 |
287.918076 |
728.096616 |
We can appreciate theese
results in the following log-log plot: 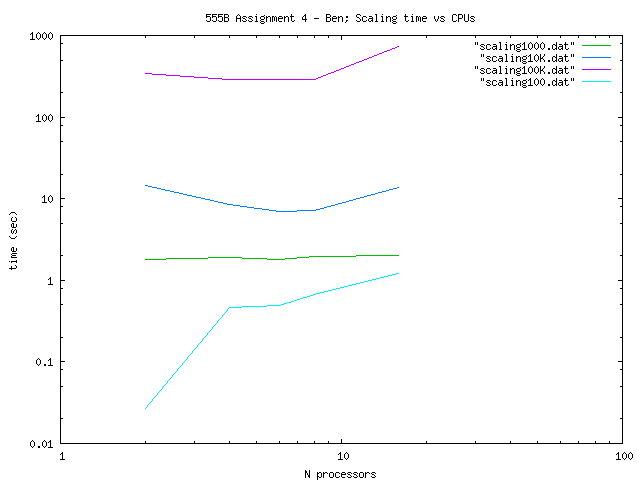
|