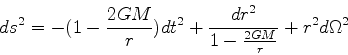The geometry

The Schwarzschild¹ spacetime [1],

$$ds^2 = -(1-\frac{2GM}{r})dt^2+\frac{dr^2}{1-\frac{2GM}{r}}+r^2 d\Omega^2$$ (1)

is the solution of Einstein's equations with spherical symmetry in vacuum, and $M$ acts as a parameter which can be interpreted as the usual Newtonian mass that we would measure by studying orbits at large distances from the gravitating source. Note that as $M \rightarrow$ 0 we recover Minkowski space, which is to be expected. Note also that the metric becomes progressively Minkowskian as we go to $r\rightarrow \infty$; this property is known as asymptotic flatness.

The fact that the Schwarzschild metric is not just a good solution, but is the unique spherically symmetric vacuum solution, is known as Birkhoff 's theorem. It is interesting to note that the result is a static metric. We did not say anything about the source except that it be spherically symmetric. Specifically, we did not demand that the source itself be static; it could be a collapsing star, as long as the collapse were symmetric. Therefore a process such as a supernova explosion, which is basically spherical, would be expected to generate very little gravitational radiation (in comparison to the amount of energy released through other channels). This is the same result we would have obtained in electromagnetism, where the electromagnetic fields around a spherical charge distribution do not depend on the radial distribution of the charges.