



Next: The Routine
Up: Visualtization Project: Geodesic Integrator
Previous: Introduction and Motivation
Contents
In terms of local coordinates on a given space-time (M) the geodesic equation can be written as [5,6,3]
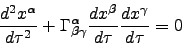 |
(1) |
The gamma symbols are of course the Christoffel connections or symbols which are, as we know, derivatives of the metric function. For that reason we will need to have access to the derivatives of the metric components. We can use a numerical differentiation but we have chosen to use maple to do this. Maple is used only to find the derivatives and then a fortran routine is used to solve the non-linear differential equations. The fortran routine is much more efficient at handling this than maple especially considering that for a simulation with dust many many operations will take place.
In the first assignment we solved this for the special case of the Schwarzschild space-time in a place and we would like to extend this to more general situations.
The non-zero Christoffel
symbols for Schwarzschild. We calculated them using Maple and
GRTensor:
(1) which turns into the following four equations, using spherical
coordinates where 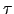 is an
affine parameter1:
is an
affine parameter1:




Next: The Routine
Up: Visualtization Project: Geodesic Integrator
Previous: Introduction and Motivation
Contents
Benjamin Gutierrez
2005-07-24
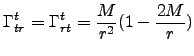

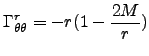
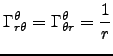
![]() is an
affine parameter1:
is an
affine parameter1: