We will simplify the geodesics equations (6) obtained in
the preceeding section restricting the motion of our massive particle
to the plane ![]() . In addition, we need to cast our
equations in first order form, so they have a suitable form to be
integrated by the LSODA routine. Introducing the variables
. In addition, we need to cast our
equations in first order form, so they have a suitable form to be
integrated by the LSODA routine. Introducing the variables
![]() and
and ![]() we accomplish this task (where the
dot indicates derivative with respect to
we accomplish this task (where the
dot indicates derivative with respect to ![]() ),
),
| (19) |
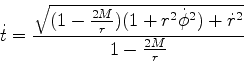 |
(20) |
orbit <L2> <R0> <Rdot0> <dtau> <tau_f>The output data will be visualized in two ways: a two-dimensional graph plotted by gnuplot and and the data will also be output in a format suitable for pp2d or xfpp3d (we include a few screenshots of animations).
We also coded the subroutine fcn in two ways: the first
implementation incorporated the equations of motion in first order
form as we saw in (19), and we also used a maple procedure
to output the Christoffel symbols as a fortran 77 subroutine. We
included the subroutine cg0 in our code and then we coded a general form
of the geodesic equations:
The code also produces error messages when the integrator crashes,
which occurs when the particle gets close to the eventhorizon or the
origin (the geodesic equations become singular of course). The gnuplot
script also uses grep and awk to filter messages from
usefull data. We leave the mass of the particle, ![]() , as a parameter
declared in our fcn subroutine.
, as a parameter
declared in our fcn subroutine.
Finally, to monitor the stability of the solution we calculate the
constans of motion of the geodesic , the square of the angular
momentum and the energy:
| (21) |
lnx1 87> orbit 4.0 2.0 0.0 0.01 30
Integration completed successfully.
Conserved quantities:
E =
1.000000000000000
maxError E =
2.2056483306442942E-009
L2 =
4.000000000000000
maxErrorL2 =
6.4374858776972133E-009
Larger tolerances produce errors in LSODA. So we sticked to this
tolerance for most of the experiments. We are aware that some orbits
must be more sensitive to this parameter than others, but variating
the tolerance did not seem to modify the orbits in any significant way.